5 класс. Математика. Никольский, Потапов. Учебник. Упражнение 440
Ответы к упражнению 440
Касательной к окружности называют прямую, имеющую с окружностью только одну общую точку. Эту точку называют точкой касания. На рисунке 80 изображены окружность с центром O, касательная AB и радиус окружности OC. C − точка касания.
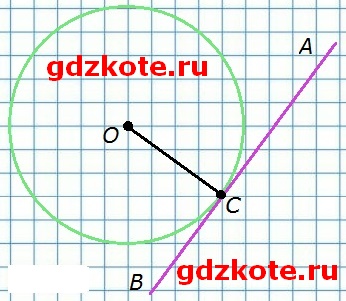
а) Определите углы, образованные касательной и радиусом окружности, проведенным в точку касания.
Углы (∠ОСВ и ∠ОСА), образованные касательной и радиусом окружности , проведенным в точку касания, являются прямыми.
б) Покажите, как должны располагаться две окружности, чтобы они имели α общих касательных? Рассмотрите все возможные случаи: α = 0, 1, 2, 3, 4.
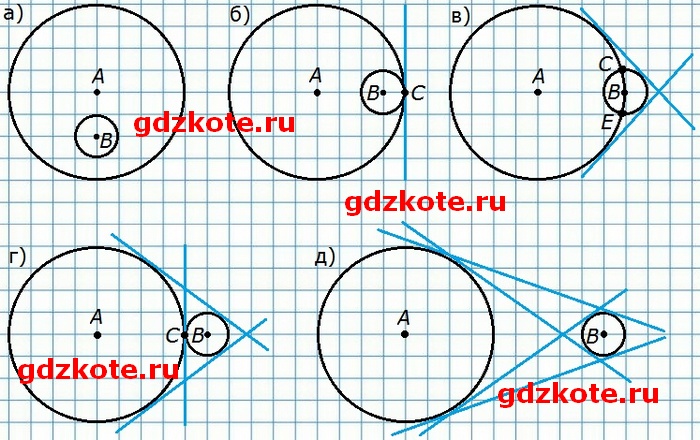
а = 0. Если одна из окружностей целиком лежит внутри другой, то общих касательных у них нет.
а = 1. Если окружности имеют единственную общую точку, касаясь внутренним образом, то касательная одна.
а = 2. Если окружности имеют две общие точки, то общих касательных две.
а = 3. Если окружности имеют единственную общую точку, касаясь внешним образом, то касательных три.
а = 4. Если каждая из окружностей лежит вне другой, и они не имеют общих точек, то окружности имеют четыре общих касательных.