5 класс. Математика. Никольский, Потапов. Учебник. Упражнение 569
Ответы к упражнению 569
Другие решебники 5 класс:
Докажите, что длина ломаной ABC больше длины ломаной ADC (рис. 118).
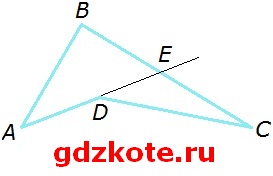
ABC = AB + BC, ADC = AD + DC.
Нужно доказать, что:
AD + DC < AB + BC.
Прибавим к обеим ломаным отрезок DE:
AB + BC + DE;
AD + DC + DE.
AD + DE = AE;
BE + EC = BC, значит:
AB + BC + DE и AE + DC.
В треугольнике длина каждой стороны меньше суммы длин двух других сторон, поэтому:
AE < AB + BE, a DC < EC + DE, значит:
AE + DC < (AB + BE) + (EC + DE).
AE = AD + DE, а BC = BE + EC, поэтому:
AD + DE + DC < AB + BC + DE.
Теперь вычтем DE:
AD + DC < AB + BC, что и требовалось доказать.