5 класс. Математика. Никольский, Потапов. Учебник. Упражнение 572
Ответы к упражнению 572
Отрезок, соединяющий две несоседние вершины многоугольника, называют диагональю многоугольника. Например, в четырёхугольнике ABCD отрезка AC и BD – диагонали (рис. 119).
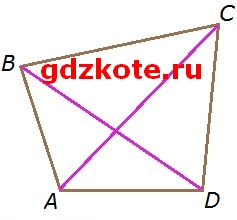
Пусть многоугольник имеет n вершин. Тогда из каждой вершины выходит (n – 3) диагоналей: 1 – сама вершина и 2 – соседние вершины.
Так как диагональ соединяет 2 вершины, значит необходимо (n – 3) разделить пополам и умножить на количество вершин, тогда мы получим, что количество диагоналей n-угольника можно найти так: n * (n – 3) : 2.
Сколько диагоналей в выпуклом:
а) четырёхугольнике;
4 * (4 – 3) : 2 = 4 * 1 : 2 = 4 : 2 = 2 диагонали.

б) пятиугольнике;
5 * (5 – 3) : 2 = 5 * 2 : 2 = 10 : 2 = 5 диагоналей.

в) шестиугольнике;
6 * (6 – 3) : 2 = 6 * 3 : 2 = 18 : 2 = 9 диагоналей.

г) семиугольнике?
7 * (7 – 3) : 2 = 7 * 4 : 2 = 28 : 2 = 14 диагоналей.
