5 класс. Математика. Никольский, Потапов. Учебник. Упражнение 577
Ответы к упражнению 577
Другие решебники 5 класс:
Считают, что если многоугольники равны, то их площади равны; если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей составляющих его многоугольников. На рисунке 121 изображен прямоугольник ABCD. Верно ли, что площади треугольников ABD и CDB равны? Чему равна площадь треугольника ABD?
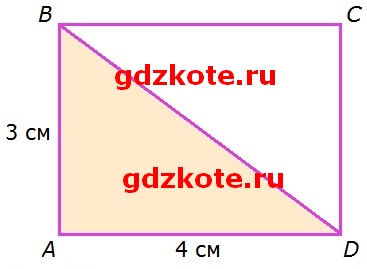
В прямоугольнике противолежащие стороны равны, а диагональ относится к обоим треугольникам, поэтому верно, что площади треугольников ABD и CDB равны.
Площадь треугольника ABD будет равно половине площади прямоугольника ABCD:
3 * 4 : 2 = 12 : 2 = 6 (см2)
Ответ: площадь треугольника ABD — 6 см2.