4 класс. Математика. Моро, Бантова. Учебник. Часть 1. Страница 61
Ответы к странице 61
267.

268. Проверь, верны ли равенства.
7 км 080 м = 70 800 м — неверно
(7 км 080 м = 7 000 м + 80 м = 7 080 м)
10 т 300 кг = 10 300 г — неверно
(10 г 300 кг = 10 000 кг + 300 кг = 10 000 000 + 300 000 = 10 300 000 г)
3 м2 = 20 000 см2 — неверно
(3 м2 = 3 * 100 см * 100 см = 30 000 см2)
4 ч = 100 мин — неверно
(4 ч = 4 * 60 = 240 мин)
8 мин 20 c = 500 с — верно
(8 мин 20 с = 8 * 60 + 20 = 480 + 20 = 500 с)
20 км2 = 20000000 м2 — верно
(20 км2 = 20 * 1 000 м * 1 000 м = 20000000 м2)
269. (Устно.) Заполни пропуски.
в 1 тысяче 10 сотен;
B 1 сотне 10 десятков;
в 1 десятке 10 единиц;
в 1 миллионе 10 сотен тысяч;
в 1 сотне тысяч 10 десятков тысяч;
в 1 десятке тысяч 10 тысяч.
270. В январе фабрика выпустила 4850 т бумаги, а в феврале — на 365 т меньше. Из всей этой бумаги 6335 т пошло на изготовление общих тетрадей, а из остальной бумаги сделали тонкие тетради. Поставь вопрос и реши задачу.
Сколько сделали тонких тетрадей?
1) 4 850 — 365 = 4 485 (т) — бумаги сделали в феврале.
2) 4 850 + 4 485 = 9 335 (т) — бумаги сделали в январе и феврале.
3) 9 335 — 6 335 = 3 000 (т) — бумаги пошло на изготовление тонких тетрадей.
Ответ: 3000 т.
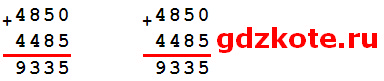
271. Садовод разбил фруктовый сад прямоугольной формы. Ширина сада 50 м, а длина в 2 раза больше ширины. Сколько деревьев можно посадить на этой площади, если отводить на одно дерево 10 м2?
1) 50 * 2 = 100 (м) — длина сада.
2) 50 * 100 = 5 000 (м2) — площадь сада.
3) 5 000 : 10 = 500 (дер.) — можно посадить на этом участке.
Ответ: 500 деревьев.
272. Найди частное и остаток. Выполни проверку.

273. В 100 одинаковых вагонах можно перевезти 6000 т угля. B трёх таких вагонах помещается столько угля, сколько в двух большегрузных вагонах. Сколько тонн угля в одном большегрузном вагоне?
1) 6 000 : 100 = 60 (т) — грузоподъёмность одного вагона.
2) 60 * 3 = 180 (т) — грузоподъёмность трёх вагонов.
3) 180 : 2 = 90 (т) — грузоподъёмность большегрузного вагона.
Ответ: 90 т.
274.
10 106 − (8 508 − 3 469) = 10 106 — 5 039 = 5 067

(1 000 + 200) : (20 * 5) = 1 200 : 100 = 12
275. Какая доля каждой фигуры закрашена?

В первой фигуре всего 12 клеток, а закрашено — 6 клеток, значит 12 : 6 = 2; закрашена половина фигуры.
Во второй фигуре всего 16 клеток, а закрашено 4 клетки, значит 16 : 4 = 4; закрашена четверть фигуры.
Задание под знаком вопроса.
31 010 − (5 000 − 3 774) = 31 010 — 1 226 = 29 784

(4 000 − 500 : 100) * 10 = (4 000 — 5) * 10 = 3 995 * 10 = 39 950