4 класс. Математика. Моро, Бантова. Учебник. Часть 2. Страница 64
Ответы к странице 64
256.

90 000 — 705 * 83 = 90 000 — 58 515 = 31 485

80 100 — 603 * 79 = 80 100 — 47 637 = 32 463

257. Реши задачи и сравни их решения.
1) Длина водохранилища 600 км, а его ширина 400 км. Поездка на катере через водохранилище по его длине занимает на 10 ч больше, чем по ширине. За сколько времени при одинаковой скорости можно пересечь водохранилище по его длине и по ширине?
1) 600 – 400 = 200 (км) — расстояние, которое может пройти катер за 10 ч.
2) 200 : 10 = 20 (км/ч) — скорость катера.
3) 600 : 20 = 30 (ч) — время поездки по длине водохранилища.
4) 400 : 20 = 20 (ч) — время поездки по ширине водохранилища.
Ответ: 30 ч, 20 ч.
2) Длина водохранилища на 200 км больше его ширины. Поездка на катере с одинаковой скоростью через водохранилище по его длине занимает 30 ч, а по ширине — 20 ч. Найди долину и ширину этого водохранилища.
1) 30 – 20 = 10 (ч) — время, за которое катер может пройти 200 км.
2) 200 : 10 = 20 (км/ч) — скорость катера.
3) 20 * 30 = 600 (км) — длина водохранилища.
4) 20 * 20 = 400 (км) – ширина водохранилища.
Ответ: 600 км, 400 км.
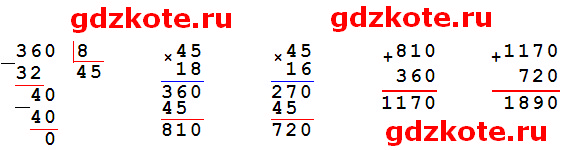
258. В питомнике вырастили саженцы деревьев: елей было 360, а на каждые 8 елей приходилось 18 клёнов и 16 лип. Сколько всего елей, клёнов и лип вырастили в питомнике?
1) 360 : 8 = 45 (раз) — по 8 елей в питомнике.
2) 45 * 18 = 810 (д.) — клёнов в питомнике.
3) 45 * 16 = 720 (д.) — лип в питомнике.
4) 360 + 810 + 720 = 1 170 + 720 = 1 890 (д.) — всего в питомнике.
Ответ: 1 890 деревьев.
259.
2 ц 50 кг * 4 = 250 ц * 4 = 1 000 кг = 1 т
125 м * 8 = 1 000 м = 1 км
1 м 20 см * 6 = 120 см * 6 = 720 см = 7 м 20 см
1 м 20 см : 6 = 120 см : 6 = 20 см
2 мин 30 с * 5 = 150 с * 5 = 750 с = 12 мин 30 с
2 ч 30 мин : 5 = 150 мин : 5 = 30 мин
260. Запиши неравенства и объясни, почему они верны.
1) Сумма чисел 289 и 1 больше их произведения.
(289 + 1) > 289 * 1
(290 > 289)
2) Сумма чисел 289 и 0 больше их произведения.
289 + 0 > 289 * 0
(289 > 0)
3) Частное чисел 289 и 1 больше их разности.
289 : 1 > 289 – 1
(289 > 288)
261. Реши те уравнения, в которых неизвестное находят умножением.
| x : 100 = 90 x = 90 * 100 x = 9 000 |
x : 18 = 30 x = 30 * 18 x = 540 |
262. Докажи, что в каждой окружности все диаметры делятся центром окружности на 2 равных отрезка.
Известно, что диаметр равен двум радиусам, а все радиусы в окружности равны. Значит, диаметр делится центром окружности на 2 равных отрезка.
263.
17 256 — 256 * 3 = 17 256 — 768 = 16 488

38 007 — 603 : 9 = 38 007 — 67 = 37 940

(205 167 — 123 068) * 7 = 82 099 * 7 = 574 693
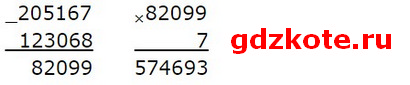
(31 280 + 14 320) * 6 = 45 600 * 6 = 273 600
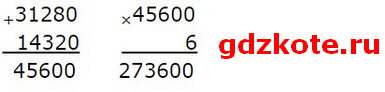
264. Школьная хоккейная площадка длиной 50 м и шириной 20 м обнесена бортиком прямоугольной формы высотой 1 м. Сколько краски потребуется для окраски бортика с внешней и внутренней сторон, если расход краски на 1 м2 составляет 140 г и краска должна быть нанесена в 2 слоя?
1) (50 + 20) * 2 = 140 (м) — периметр бортика площадки.
2) 140 * 1 = 140 (м2) — площадь бортика с одной стороны.
3) 140 * 2 = 280 (м2) — площадь бортика с обоих сторон.
4) 280 * 140 = 39 200 (г) — расход краски в один слой.
5) 39 200 * 2 = 78 400 = 78 (кг) 400 (г) — необходимо всего краски.
Ответ: 78 кг 400 г.

Задание под знаком вопроса (под чертой).
Вычисли.
5 м 30 см * 6 = 30 м + 180 см = 30 м + 1 м 80 см = 31 м 80 см
Задание на полях.
Ребус.
