4 класс. Математика. Моро, Бантова. Учебник. Часть 2. Страница 76
Ответы к странице 76
308. Проверь, правильно ли выполнено деление с остатком.
1) 70 537 : 54 = 1 306 (ост. 17)
1 306 * 54 + 17 = 70 524 + 17 = 70 541 — неверно
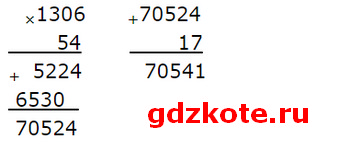
2) 33 367 : 164 = 203 (ост. 75)
203 * 164 + 75 = 33 292 + 75 = 33 367 — верно
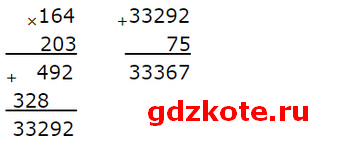
3) 155 364 : 604 = 257 (ост. 136)
257 * 604 + 136 = 155 228 + 136 = 155 364 — верно

309. Найди делимое, если известно, что:
1) делитель 34, частное 8 050, остаток 12;
8 050 * 34 + 12 = 273 700 + 12 = 273 712

2) делитель 46, частное 3 080, остаток 35.
Проверь, выполнив деление.
3 080 * 46 + 35 = 141 680 + 35 = 141 715

310. Два опытных участка имеют одинаковую площадь. Ширина первого участка 60 м, а ширина второго 80 м. Найди длину первого участка, если известно, что длина второго участка 150 м. Сделай по задаче чертёж и реши задачу.
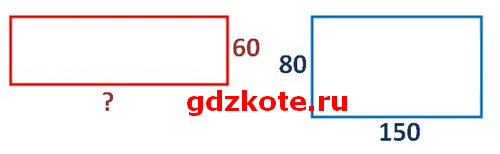
1) 150 * 80 = 12 000 (м2) — площадь второго участка (и первого участка).
2) 12 000 : 60 = 200 (м) — длина первого участка.
Ответ: 200 м.
311. Одна бригада рабочих может заасфальтировать 15 км шоссейной дороги за 30 дней, а другая — за 60 дней. За сколько дней могут заасфальтировать эту дорогу обе бригады, работая вместе?
15 км = 15 000 м
1) 15 000 : 30 = 500 (м) — асфальтирует первая бригада за 1 день.
2) 15 000 : 60 = 250 (м) — асфальтирует вторая бригада за 1 день.
3) 500 + 250 = 750 (м) — асфальтируют бригады вместе.
4) 15 000 : 750 = 20 (д.) — потребуется.
Ответ: за 20 дней.

312. Поезд отправился из Санкт-Петербурга в 23 ч 15 мин и прибыл в Москву в 6 ч 25 мин следующего дня. По пути он сделал 2 остановки: на станции Бологое и в городе Твери, по 5 мин каждая. С какой скоростью двигался этот поезд, если он прошёл 651 км?
1) 24 ч — 23 ч 15 мин = 45 (мин) — был в пути поезд в первый день.
2) 6 ч 25 мин + 45 мин = 7 (ч) 10 (мин) — общее время в пути.
3) 7 ч 10 мин — (5 мин + 5 мин) = 7 (ч) — время в пути без остановок.
4) 651 : 7 = 93 (км/ч) — скорость движения поезда
Ответ: 93 км/ч

313. Вычисли и выполни проверку.

314. Реши уравнения.
| x — 640 = 921 : 3 x — 640 = 307 x = 307 + 640 x = 947  |
x : 9 = 2 007 : 9 x : 9 = 223 x = 223 * 9 x = 2 007  |
x * 81 = 729 : 3 x * 81 = 243 x = 243 : 81 x = 3  |
315. Как налить 5 л воды, используя десятилитровое ведро и трёхлитровую банку?
3 раза вылить воду из банки в ведро — в ведре станет 9 литров воды. Долить воды в ведро доверху, тем самым мы нальем в ведро 1 литр воды, а в банке останется 2 литра воды. Вылить из ведра всю воду и залить в ведро те два литра из банки. Долить еще одну полностью заполненную банку. Таким образом, в ведре будет ровно 5 литров воды.
Задание под знаком вопроса (под чертой).
Периметр прямоугольника 11 дм 4 см, а длина одной его стороны 3 дм 2 см. Найди длину другой стороны этого прямоугольника.
11 дм 4 см = 11 * 10 + 4 = 114 см
1) 114 : 2 = 57 см = 5 дм 7 см — длина двух сторон прямоугольника.
2) 5 дм 7 см — 3 дм 2 см = 2 дм 5 см — длина другой стороны.
Ответ: 2 дм 5 см.

Задание на полях.
Ребус.
