4 класс. Математика. Моро, Бантова. Учебник. Часть 2. Страница 96
Ответы к странице 96
1. Назови знакомые тебе геометрические фигуры, начерти их в тетради и обозначь буквами.
2. Что ты знаешь о многоугольниках? Сколько вершин, углов и сторон у двенадцатиугольника?
Многоугольники называют по числу углов. Если в многоугольнике 3 угла — это треугольник, если 4 — это четырехугольник, если 5 — пятиугольник и т.д. В любом многоугольнике число углов равно числу сторон и вершин.
В двенадцатиугольнике 12 углов, 12 вершин и 12 сторон.
3. Какие виды треугольников ты знаешь? Может ли прямоугольный треугольник быть равносторонним? разносторонним? Может ли тупоугольный треугольник быть равнобедренным? Начерти в тетради равнобедренный прямоугольный треугольник.
От вида углов треугольники бывают: остроугольные, тупоугольные и прямоугольные.
В зависимости от длин сторон треугольники бывают: разносторонние, равносторонние, равнобедренные.
Прямоугольный треугольник не может быть равносторонним, но может быть разносторонним или равнобедренным.
Тупоугольный треугольник может быть равнобедренным.
4. Какие виды четырёхугольников ты знаешь? Продолжи предложения:
1) Прямоугольник — это четырехугольник, у которого все углы прямые, а противоположные стороны равны между собой.
2) Квадрат — это прямоугольник, у которого все стороны равны.
5.
1) Среди четырёхугольников, изображённых на рисунке 1, найди прямоугольники и запиши их названия; подчеркни название квадрата.
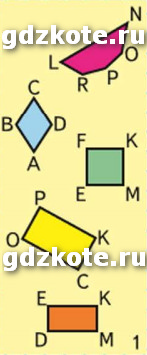
EFKM, ОРКС, DEKM.
2) Найди периметр прямоугольника ОРКС и площадь квадрата. Объясни, почему четырёхугольник ABCD нельзя назвать квадратом.
Периметр прямоугольника ОРКC: 2 * (15 + 9) = 48 мм.
Площадь квадрата KMEF: 9 * 9 = 81 м2.
Четырехугольник ABCD нельзя назвать квадратом, так как он не прямоугольник, хотя его стороны и равны.
6. Определи вид каждого треугольника, если его периметр находят так:
1) 3 + 4 + 5 = 12 (см);
разносторонний треугольник, т.к. все стороны разные.
2) 3 * 2 + 4 = 10 (см);
равнобедренный треугольник, т.к. 2 стороны равны.
3) 5 * 3 = 15 (см).
равносторонний треугольник, т.к. все стороны равны.
7. Рассмотри рисунок 2 на полях и запиши названия всех прямоугольных, остроугольных и тупоугольных треугольников; подчеркни названия равнобедренных треугольников.
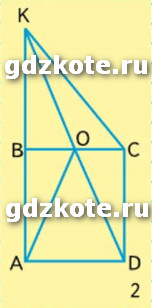
Прямоугольные треугольники: KBC, KBO, ABO, OCD, KAD.
Остроугольный треугольник: AOD.
Тупоугольные треугольники: KOC, AOK, KCD.
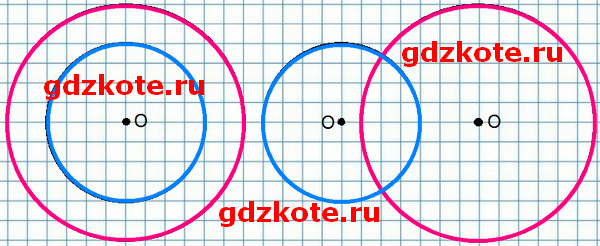
8. Начерти 2 окружности с радиусами 2 см и 3 см сначала с общим центром, а потом с разными центрами.
9. Найди длину ломаной АОKC (рис. 2).
Длина ломанной АОКС: 30 + 32 + 39 = 101 мм.