5 класс. Математика. Виленкин. Учебник. Часть 1. Упражнение 4.160
Ответы к упражнению 4.160
Прямоугольный параллелепипед (рис. 4.31) состоит из двух частей.
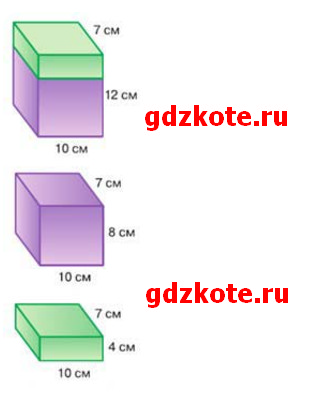
а) Вычислите объем параллелепипеда и его частей. Равен ли объем параллелепипеда сумме объемов его частей?
1) 10 · 12 · 7 = 120 · 7 = 840 (см³) – объем всего параллелепипеда
2) 10 · 8 · 7 = 10 · 56 = 560 (см³) – объем фиолетовой части
3) 10 · 4 · 7 = 10 · 28 = 280 (см³) – объем зеленой части
4) 560 + 280 = 840 (см³) – общий объем зеленой и фиолетовой частей
5) 840 см³ = 840 см³ – объем параллелепипеда равен сумме объемов его частей
Ответ: да, равен.
б) Вычислите площадь поверхности параллелепипеда и его частей. Равны ли площади поверхности параллелепипеда и сумма площадей поверхностей его частей? Объясните почему.
1) 2 · (10 · 12 + 12 · 7 + 10 · 7) = 2 · (120 + 84 + 70) = 2 · 274 = 548 (см²) – площадь поверхности всего параллелепипеда
2) 2 · (10 · 8 + 8 · 7 + 10 · 7) = 2 · (80 + 56 + 70) = 2 · 206 = 412 (см²) – площадь поверхности фиолетовой части
3) 2 · (10 · 4 + 4 · 7 + 10 · 7) = 2 · (40 + 28 + 70) = 2 · 138 = 276 (см²) – площадь поверхности зеленой части
4) 412 + 276 = 688 (см²) – общая площадь зеленой и фиолетовой частей
5) 548 см² < 688 см² – сумма площадей частей параллелепипеда больше площади самого параллелепипеда
Ответ: нет, не равны (в площади поверхности параллелепипеда не учитывается площадь соприкасающихся частей)