4 класс. Математика. Моро, Бантова. Учебник. Часть 2. Страница 41
Ответы к странице 41
4. Одна открытка, 2 одинаковых конверта и 3 одинаковые марки стоят 38 р. Три такие открытки, 2 таких конверта и 1 такая же марка стоят 22 р. Сколько стоит набор из открытки, конверта и марки?
Из условия задачи очевидно, что 4 открытки, 4 конверта и 4 марки (т.е. 4 набора) стоят 38 + 22 = 60 р.
Значит один набор стоит: 60 : 4 = 15 (р.)
Ответ: 15 рублей.
5. Занимательные рамки. Магический квадрат.
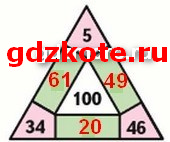
34 + 61 + 5 = 100
5 + 49 + 46 = 100
46 + 20 + 34 = 100

260 + 540 + 200 = 1 000
550 + 280 + 170 = 1 000
260 + 190 + 550 = 1 000
200 + 630 + 170 = 1 000

18 + 15 + 15 = 48
17 + 15 + 16 = 48
17 + 15 + 16 = 48
16 + 15 + 17 = 48
Свои задачи.
1. Арифметические задания.
1. Запиши число 7 при помощи четырех троек и знаков действий. Найди несколько решений.
7 = 3 : 3 + 3 + 3
7 = 3 + 3 + 3 : 3
7 = 3 + 3 : 3 + 3
2. Три брата поймали 29 карасей. Когда один брат отложил для ухи 6 штук, другой — 2, а третий – 3, то у каждого осталось равное количество рыб. Сколько карасей поймал каждый из них?
1) 6 + 2 + 3 = 11 (к) — ушло на уху.
2) 29 — 11 = 18 (к) — осталось всего.
3) 18 : 3 = 6 (к) — осталось у каждого брата.
4) 6 + 6 = 12 (к) – было у первого брата.
5) 6 + 2 = 8 (к) — было у второго брата.
6) 6 + 3 = 9 (к) – было у третьего брата.
Ответ: 12, 8 и 9 карасей соответственно.
3. Сколько четырёхместных лодок понадобится, чтобы перевезти одновременно 18 человек?
1) 18 : 4 = 4 ост 2
Ответ: понадобится 5 лодок (4 по 4 человека и одна 2 человека).
2. Геометрические задачи.
1. Докажите, что шахматную доску 10×10 нельзя покрыть фигурками следующего вида:
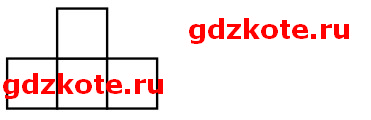
Ответ: Каждая фигурка указанного вида покрывает три клетки одного цвета и одну клетку другого (три клетки чёрного цвета и одну белого, или наоборот). Поскольку всего на шахматной доске чёрных и белых клеток поровну, то количество фигурок, содержащих три белые клетки и одну чёрную, должно совпадать с количеством фигурок, содержащих три чёрные клетки и одну белую. Следовательно, общее количество фигурок должно быть чётным. Однако это невозможно, так как общее количество фигурок равно 100 : 4 = 25.
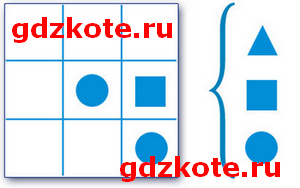
2. В каждую клетку квадрата 3×3 надо вписать одну из геометрических фигур: круг, квадрат или треугольник. Каждая фигура должна встречаться в каждой строчке и в каждом столбце. Заполните пустующие клетки.
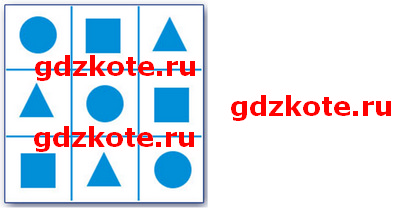
3. Домик Кролика нарисован 4 раза, а домик Пятачка только один раз. Где домик Пятачка?
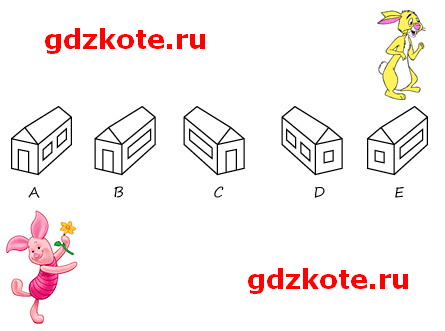
Предположим, что кролик живет в домике (Е). Тогда домик (D) – тот же домик, но повернут так, что видна левая стенка.
А домик (С), – это домик (Е), если смотреть на него со стороны входа.
Домик (В) – не домик Кролика, так как правая его стена имеет одно окно, а правая стена от входа домика Кролика (смотрим на домик (D)) имеет два окошка.
А вот домик (А) – домик Кролика: это домик (D), если смотреть на него со стороны входа.
Итак, у Кролика четыре домика: (А), (С),(D) и (Е), а (В) – домик Пятачка.
Ответ: В.
3. Текстовые задачи.
1. У одного старика спросили, сколько ему лет. Он ответил, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25. Как это могло быть?
Ответ: этот человек родился 29 февраля, т. е. день рождения у него бывает один раз в четыре года.
2. В 12-этажном доме есть лифт. На первом этаже живет всего 2 человека, от этажа к этажу количество жильцов увеличивается вдвое. Какая кнопка в лифте этого дома нажимается чаще других?
Ответ: независимо от распределения жильцов по этажам, кнопка «1».
3. На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты?
Ответ: 2 рубля и 1 рубль (если одна из них — не 1 рубль, то другая монета — 1 рубль).