4 класс. Математика. Моро, Бантова. Учебник. Часть 2. Страница 56
Ответы к странице 56
Что узнали. Чему научились.
22. От двух пристаней, расстояние между которыми 350 км, в 11 ч отправились навстречу друг другу два теплохода. Скорость первого 32 км/ч, скорость второго 38 км/ч. В какое время теплоходы встретятся?
1) 32 + 38 = 70 (км/ч) — скорость сближения теплоходов.
2) 350 : 70 = 5 (ч) — время до встречи теплоходов.
3) 11 + 5 = 16 (ч) — в это время они встретятся.
Ответ: в 16 часов.
23. Два велосипедиста отправились из одного посёлка одновременно в противоположных направлениях. Через 30 мин расстояние между ними было 15 км. Скорость одного из них 260 м/мин. Узнай скорость другого велосипедиста. (Вырази 15 км в метрах.)
Составь и реши задачи, обратные данной.
15 км = 15000 м
1) 260 * 30 = 7 800 (м) — проехал первый велосипедист.
2) 15 000 – 7 800 = 7 200 (м) — проехал второй велосипедист.
3) 7 200 : 30 = 240 (м/мин) — скорость второго велосипедиста.
Ответ: 240 м/мин.
Обратная задача 1:
Два велосипедиста отправились из одного посёлка одновременно в противоположных направлениях. Скорость одного из них 260 м/мин, а другого — 240 м/мин. Какое расстояние будет между ними через 30 мин?
1) 260 + 240 = 500 (м/мин) — скорость удаления велосипедистов.
2) 500 * 30 = 15 000 (м) = 15 (км) — расстояние между велосипедистами через 30 мин.
Ответ: 15 км.
Обратная задача 2:
Два велосипедиста отправились из одного посёлка одновременно в противоположных направлениях. Скорость одного из них 260 м/мин, а другого — 240 м/мин. Через какое время расстояние между ними будет 15 км?
1) 260 + 240 = 500 (м/мин) — скорость удаления велосипедистов.
2) 15 000 : 500 = 30 (мин) — через столько времени расстояние между велосипедистами будет 15 км.
Ответ: 30 мин.
24. в санатории построили бассейн прямоугольной формы, длина которого 15 м, ширина 5 м и глубина 2 м.
1) Сколько квадратных кафельных плиток со стороной 1 дм каждая потребовалось для облицовки дна этого бассейна? стенок этого бассейна?
1) 15 * 5 = 75 (м2) = 7 500 (дм2) — площадь дна бассейна.
2) 1 * 1 = 1 (дм2) — площадь одной плитки.
3) 7 500 : 1 = 7 500 (пл.) — нужно для облицовки дна бассейна.
4) 2 * (15 * 2) + 2 * (5 * 2) = 2 * 30 + 2 * 10 = 60 + 20 = 80 (м2) = 8000 (дм2) — площадь всех стенок бассейна.
5) 8 000 : 1 = 8 000 (пл.) — нужно для облицовки стен бассейна.
Ответ: 7500 плиток для дна и 8000 плиток для стен.
2) Сколько надо сделать шагов, чтобы обойти весь бассейн, если длина шага 50 см?
1) (15 + 5) * 2 = 20 * 2 = 40 (м) = 4 000 (см) — периметр дна бассейна.
2) 4 000 : 50 = 80 (ш.) — надо сделать.
Ответ: 80 шагов.
25. Составь по данной таблице выражения, которые показывают:
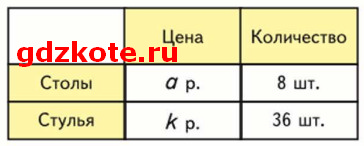
1) стоимость всех купленных столов и стульев;
8 * a + 36 * k
2) на сколько больше стоимость всех стульев, чем стоимость всех столов;
36 * k – 8 * a
3) стоимость всех столов и шести стульев.
8 * a + 6 * k
Вопросы для повторения
1. Объясни на примере, как можно по-разному умножить число на сумму.
1) 3 * (2 + 4) = 3 * 6 = 18
2) 3 * (2 + 4) = 3 * 2 + 3 * 4 = 6 + 12 = 18
2. Составь примеры на умножение двузначного числа на двузначное и трёхзначного числа на трёхзначное. Реши их с объяснением.

Умножу первый множитель на число единиц:
68 * 4 = 272
Получу первое неполное произведение: 272.
Умножу первый множитель на число десятков:
68 * 2 = 136
Получу второе неполное произведение: 136.
Начну подписывать второе неполное произведение под десяткам Сложу неполные произведения.
Читаю ответ: 1 632. Это произведение чисел 68 и 24.
Умножу первый множитель на число единиц:
812 * 6 = 4 872
Получу первое неполное произведение: 4 872.
Умножу первый множитель на число десятков:
812 * 4 = 3 248
Получу второе неполное произведение: 3 248.
Начну подписывать второе неполное произведение под десятками. Умножу первый множитель на число сотен:
812 * 2 = 1 624
Получу третье неполное произведение: 1 624.
Начну подписывать третье неполное произведение под десятками второго неполного произведения.
Сложу неполные произведения.
Читаю ответ: 199 752. Это произведение чисел 812 и 246.