4 класс. Математика. Моро, Бантова. Учебник. Часть 2. Страница 55
Ответы к странице 55
Что узнали. Чему научились.
12. Сравни скорости, с которыми могут двигаться разные животные (с. 78—79).
1. 600 м/мин = 600 * 60 = 36000 м/ч = 36 км/ч − скорость аиста.
2. 90 км/ч − скорость голубя.
3. 60 км/ч − скорость воробья.
4. 72 км/ч − скорость колибри.
5. 30 м/с = 30 * 3 600 = 108 000 м/ч = 108 км/ч − скорость гепарда.
6. 25 м/с = 25 * 3 600 = 90 000 м/ч = 90 км/ч − скорость антилопы.
7. 80 км/ч − скорость льва.
8. 500 м/мин = 500 * 60 = 30 000 м/ч = 30 км/ч − скорость страуса.
9. 1 км/мин = 1 * 60 = 60 км/ч − скорость зебры.
10. 750 м/мин = 750 * 60 = 45 000 м/ч = 45 км/ч − скорость жирафа.
13.
1) Дана сумма 36 + 44. Каждое слагаемое увеличили в 20 раз. Проверь, увеличится ли в 20 раз значение суммы.
36 + 44 = 80
36 * 20 + 44 * 20 = 720 + 880 = 1 600
1 600 : 80 = 20 — да, увеличится
2) Дано произведение 15 * 10. Первый множитель увеличили в 4 раза, а второй оставили без изменения. Проверь, увеличится ли в 4 раза значение произведения.
15 * 10 = 150
15 * 4 = 60, 60 * 10 = 600
600 : 150 = 4 — да, увеличится
14.

34 * (120 — 3 920 : 70) = 34 * (120 — 56) = 34 * 64 = 2 176

(110 — 3 420 : 90) * 25 = (110 — 38) * 25 = 72 * 25 = 1 800

15. Выполни деление с остатком.
448 : 10 = 44 (ост. 8)
683 : 10 = 68 (ост. 3)
367 : 80 = 4 (ост. 47)
421 : 50 = 8 (ост. 21)
293 : 70 = 4 (ост. 13)

16. Составь и реши задачи по рисункам животных (с. 79).
Задача 1:
Известно, что гепард может бегать со скоростью 30 м/с, а лев — со скоростью 80 км/ч. Кто из них бегает быстрее и на сколько?
1) 30 м/с = 30 * 3 600 = 108 000 м/ч = 108 (км/ч) — скорость гепарда
2) 108 — 80 = 28 (км/ч) — гепард быстрее льва.
Ответ: гепард быстрее льва на 28 км/ч.
Задача 2:
Какое расстояние пробежит зебра за полчаса, если известно, что ее скорость 1 км/мин?
1 ч = 60 мин
полчаса = 60 : 2 = 30 мин.
30 * 1 = 30 (км) — пробежит зебра за полчаса.
Ответ: 30 км.
17. Реши задачи и сравни их решения.
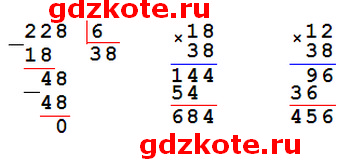
1) в один магазин привезли 18 одинаковых бидонов молока, а в другой — 12 таких же бидонов. В первый магазин привезли на 228 л молока больше, чем во второй. Сколько литров молока привезли в каждый магазин?
1) 18 — 12 = 6 (бид.) — на столько больше бидонов привезли в первый магазин.
2) 228 : 6 = 38 (л) — ёмкость одного бидона.
3) 18 * 38 = 684 (л) — молока привезли в первый магазин.
4) 12 * 38 = 456 (л) — молока привезли во второй магазин.
Ответ: 684 л и 456 л.
2) в один магазин привезли в одинаковых бидонах 684 л молока, а в другой — 456 л молока в таких же бидонах. В первый магазин привезли на 6 бидонов молока больше, чем во второй. Сколько бидонов молока привезли в каждый магазин?
1) 684 — 456 = 228 (л) — на столько литров больше привезли в первый магазин.
2) 228 : 6 = 38 (л) — ёмкость одного бидона.
3) 684 : 38 = 18 (бид.) — молока привезли в первый магазин.
4) 456 : 38 = 12 (бид.) — молока привезли во второй магазин.
Ответ: 18 бидонов и 12 бидонов.

18. Реши уравнения.
| x — 12 = 0 x = 0 + 12 x = 12 |
x : 108 = 1 x = 1 * 108 x = 108 |
x * 15 = 0 x = 0 : 15 x = 0 |
| 25 + x = 25 x = 25 — 25 x = 0 |
y : 1 = 37 y = 37 : 1 y = 37 |
x * 18 = 18 x = 18 : 18 x = 1 |
19. Начерти и вырежи 4 квадрата со стороной 4 см. Составь из них 2 разных прямоугольника и найди периметр и площадь каждого из них.
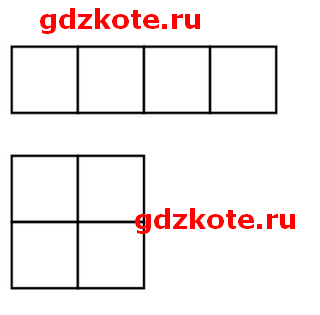
1 рисунок:
Площадь: 4 * 16 = 64 см2
Периметр: (4 + 16) * 2 = 20 * 2 = 40 см
2 рисунок:
Площадь: 8 * 8 = 64 см2
Периметр: 8 * 4 = 32 см
20. Рассмотри чертёж и выпиши названия всех треугольников с общей стороной АС; ВС.
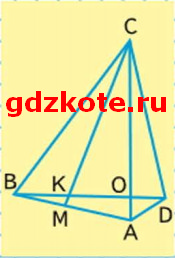
Сторона АС: АСD, АСМ, АСB.
Сторона BC: BCM, BCA, BCD, BCK, BCO.
21.
1) Объясни, почему на 2 делится без остатка любое число, в записи которого последняя цифра 0, 2, 4, 6 или 8.
Любое число, которое оканчивается на 0, 2, 4, 6 или 8 является четным. Если поделить четное число на 2, то оно всегда делится нацело (без остатка).
2) Какой должна быть последняя цифра в записи числа, которое делится без остатка на 5?
Чтобы число делилось на 5 без остатка, последняя цифра этого числа должна быть 0 или 5.
Задание на полях.
Найди лишнее выражение.
120 * 1 — лишнее, т.к. здесь используется операция умножения, а в других примерах — деление.