5 класс. Математика. Виленкин. Учебник. Часть 1. Применяем математику (страницы 156, 157)
Ответы к заданию Применяем математику на страницах 156 и 157
Номер 1.
Сколько потребуется машин грузоподъемностью 5 т для перевозки 428 рулонов линолеума шириной 15 дм и длиной 200 дм, если масса одного квадратного дециметра линолеума равна 25 г?
Краткая запись:
Грузоподъемность — 5 т = 5000 кг
Рулоны — 428 шт
Длина рулона — 15 дм
Ширина рулона — 200 дм
1 дм2 — 25 г
Количество машин — ? шт.
1) 15 · 200 = 3000 (дм2) – площадь одного рулонного линолеума
2) 428 · 3000 = 1 284 000 (дм2) – площадь 428 рулонов линолеума
3) 1 284 000 · 25 = 32 100 000 (г) = 32 100 (кг) – масса всех рулонов линолеума
5) 32 100 : 5000 = 6 (ост. 2100) — потребуется 7 машин
Ответ: 7 машин.
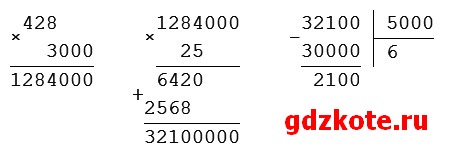
Номер 2.
Новогодний подарок упакован в коробку в форме куба с ребром 45 см (рис. 4.34). Сколько требуется ленты для обвязки крест-накрест этой коробки, если на бантик нужно еще 40 см?
1) 45 · 8 = 360 (см) – нужно ленты без бантика
2) 360 + 40 = 400 (см) = 4 (м) – нужно ленты всего
Ответ: 4 метра ленты.
Номер 3.
Из листа бумаги размером 20 х 20 см вырезали прямоугольник со сторонами 12 см и 18 см.
а) Можно ли из остатка вырезать квадрат со стороной 9 см?
1) 20 – 12 = 8 (см) – осталось по ширине
2) 20 – 18 = 2 (см) – осталось по длине
3) 8 см < 9 см и 2 см < 9 см — квадрат со стороной 9 см не получиться вырезать
Ответ: нельзя вырезать.
б) Какой квадрат наибольшей площади можно вырезать из остатка?
Можно вырезать квадрат со стороной 8 см.
Его площадь составит: 82 = 64 (см2)
Ответ: 64 см2.
Номер 4.
Вокруг прямоугольной клумбы проложили дорожку одинаковой ширины (рис. 4.35). Длина внешнего края дорожки на 16 м больше длины внутреннего. Найдите ширину дорожки.
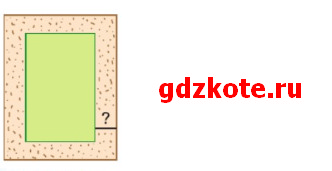
Пусть а и b ширина и длина внутреннего прямоугольника, а x ширина дорожки.
Периметр внутреннего прямоугольника: Р1 = 2а + 2b
Периметр внешнего прямоугольника: Р2 = 2 · (а + 2x) + 2 · (b + 2x)
Составим уравнение:
P2 – P1 = 16
(2a + 4x + 2b + 4x) – (2a + 2b) = 16
2a + 4x + 2b + 4x – 2a — 2b = 16
8x = 16
x = 16 : 8
x = 2 (м) – ширина дорожки
Ответ: 2 м.
Номер 5.
На рисунке 4.36 изображён план квадратного участка, по углам которого растут четыре больших дерева. Владельцы участка хотят увеличить его площадь вдвое так, чтобы деревья остались вне участка и участок остался квадратным. Возможно ли это сделать?
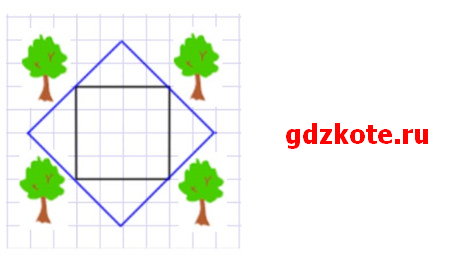
Ответ: да, это возможно.
Номер 6.
Найдите массу детали, изготовленной из стального листа (рис. 4.37), если 1 cм2 этого листа имеет массу 45 г. Размеры на рисунке даны в сантиметрах.
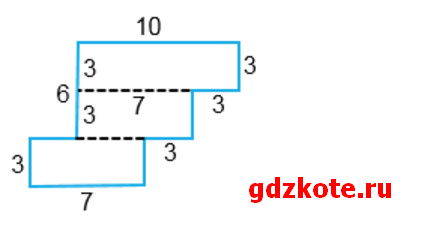
1) 10 · 3 = 30 (см2) — площадь верхнего прямоугольника
2) 7 · 3 = 21 (см2) — площади среднего и нижнего прямоугольников
3) 30 + 21 + 21 = 72 (см2) — площадь всего стального листа
4) 45 · 72 = 3240 (г) = 3 кг 240 г — масса стального листа
Ответ: 3 кг 240 г.

Номер 7.
Бабушка попросила Лену, Олю, Таню и Ярослава прополоть две квадратные клумбы, у которых стороны равны 2 м и 4 м. Ярослав решил так: маленькая клумба в 2 раза меньше большой, поэтому я выполю сорняки на маленькой клумбе и оставлю девочкам прополку большой клумбы, чтобы им было меньше полоть. Будут ли согласны девочки с таким решением?
1) 2 · 2 = 4 (м2) – площадь маленькой клумбы
2) 4 · 4 = 16 (м2) – площадь большой клумбы
3) 16 : 3 = 5 (ост. 1) – каждой девочке достанется более 5 м2
4) 4 м2 < 5 м2 – девочки прополют больше (значит, не будут согласны с решением Ярослава)
Ответ: девочки не будут согласны.
Номер 8.
Миша составил выражение для вычисления площади спортивной площадки на даче (см. план на рисунке 4.38):
(8 · 6) : 2 – 4 · 6 : 2.
Объясните его рассуждения и найдите значение этого выражения.
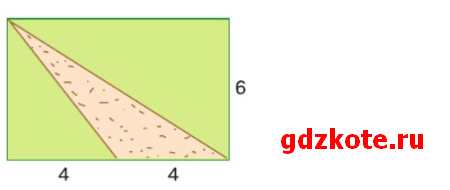
(8 · 6) — площадь всего участка
(8 — 6) : 2 — площадь участка, не занятого площадкой (справа)
4 · 6 : 2 — площадь участка, не занятого площадкой (слева)
(8 · 6): 2 — 4 · 6 : 2 — площадь спортивной площадки
(8 · 6) : 2 – 4 · 6 : 2 = 24 – 12 = 12
Ответ: 12.
Номер 9.
Рассчитайте, сколько коробок печенья надо заказать для изготовления 5300 новогодних подарков, если пачки печенья размером 10 × 6 × 4 см находятся в коробке размером 60 × 54 × 44 см, а в подарок кладут одну пачку печенья.
1) 10 · 6 · 4 = 60 · 4 = 240 (см3) — объем одной пачки печенья
2) 60 · 54 · 44 = 142 560 (см3) — объем одной коробки
3) 142 560 : 240 = 594 (п.) — печенья умещается в одной коробке
4) 5300 : 594 = 8 (ост. 548) — надо заказать 9 коробок печенья
Ответ: 9 коробок.

Номер 10.
Объём воды в озёрах земного шара около 230 000 км3.
а) Какой высоты будет башня в форме прямоугольного параллелепипеда, если его основание квадрат со стороной 0,5 м, а объём башни равен объёму воды в озёрах?
230 000 км3 = 230 000 000 000 000 м3 = 230 000 000 000 000 000 дм3
0,5 м = 5 дм
V = abc
230 000 000 000 000 000 = 5 · 5 · с
230 000 000 000 000 000 = 25с
с = 230 000 000 000 000 000 : 25
с = 9 200 000 000 000 000 (дм) = 920 000 000 000 (км) — высота башни
Ответ: 920 000 000 000 км.
б) Сравните её длину с расстоянием от Земли до Луны. Недостающие данные найдите самостоятельно.
Расстоянием от Земли до Луны: 384 400 км.
920 000 000 000 км > 384 400 км
Ответ: высота башни больше, чем расстояние от Земли до Луны.
Номер 11.
Прочитайте внимательно текст и выполните задания 1 – 6.
В начале июня Маша, Андрей и Лена приехали отдыхать к бабушке и дедушке в деревню Дальняя. Их участок (рис. 4.39) находится на пересечении улицы Солнечной и переулка Нужного. Калитка расположена со стороны переулка. Въезд машин в гараж находится со стороны улицы. При входе на участок слева от калитки находится дом, перед которым вдоль улицы растут вишни. Справа от калитки расположена хозяйственная постройка, в которой находится баня. Кроме дома, гаража и бани, есть маленький сарай для сельскохозяйственных инструментов рядом с яблоневым садом, огород, в котором располагаются теплица площадью 27 м2 и парник. Между домом и баней есть площадка, площадь которой равна 81 м2. Она замощена плиткой размером 50 х 50 см. Остальная площадь участка занята газоном, и на нём размещён батут, обозначенный цифрой 8.
Маша, Андрей и Лена решили помочь дедушке соединить дорожками шириной 1 м все хозяйственные постройки, которые планируется замостить такой же плиткой, как на площадке (на плане дорожки показаны серым цветом). А ещё они задумали разбить на газоне большую трёхъярусную клумбу, отмеченную на плане цифрой 9. На первом ярусе ребята хотят посадить тагетес (бархатцы), на втором – виолу (анютины глазки), а на третьем – агератум. Норма высадки на 1 м2 тагетеса – 60 кустиков, виолы – 70 кустиков и агератума – 80 кустиков рассады.
1. Определите на плане положение улицы и переулка.
Улица расположена слева от участка, а переулок — снизу от участка.
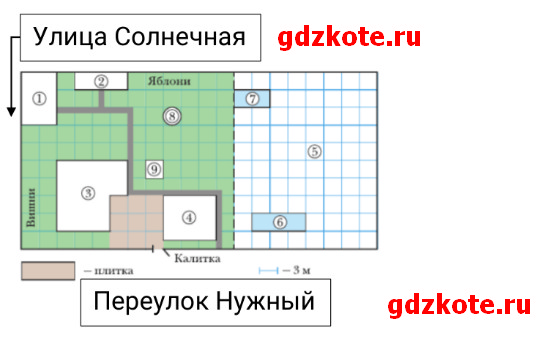
2. Определите, какими цифрами на плане обозначены объекты, и заполните таблицу.
| Объект | Дом | Гараж | Баня | Сарай | Парник | Теплица |
| Цифра | 3 | 1 | 4 | 2 | 7 | 6 |
3. Найдите площадь дома и гаража в квадратных метрах.
6 · 12 + 6 · 9 = 72 + 54 = 126 (м2) — площадь дома
6 · 9 = 54 (м2) — площадь гаража
Ответ: 54 м2.
4. Найдите расстояние от запланированной дорожки до батута.
2 ∙ 3 = 6 (м) – расстояние от запланированной дорожки до батута
Ответ: 6 метров.
5. Сколько упаковок плитки нужно купить для дорожек, если в упаковке 5 штук?
1) 12 + 3 + 15 + 15 + 9 = 54 (м) – общая длина дорожки
2) 54 ∙ 4 = 216 (пл.) – понадобится
3) 216 : 5 = 43 (ост.1) – нужно 44 упаковки
Ответ: 44 упаковки плиток.

6. Определите размер клумбы. Сколько кустиков каждой рассады надо заказать для клумбы, план которой представлен на рисунке 4.40?
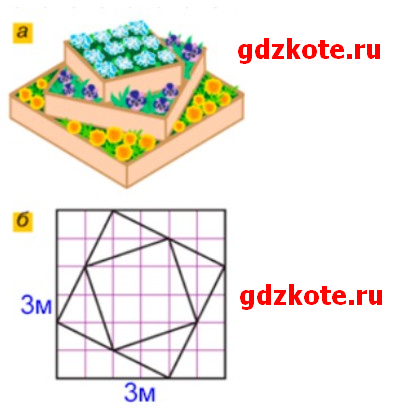
Первый ярус — 4 треугольника со сторонами 1 м и 2 м.
Третий ярус — квадрат со стороной 1 м и 4 треугольника со сторонами 150 см и 50 см.
1) 3 ∙ 3 = 9 (м2) = 90 000 (см2) – площадь всей клумбы
2) (2 ∙ 1) ∙ 2 = 4 (м2) = 40 000 (см2) – площадь первого яруса (под тагетесы)
3) 60 ∙ 4 = 240 (куст.) – тагетесов
4) (100 ∙ 100) + (150 ∙ 50) ∙ 2 = 10 000 + 15 000 = 25 000 (см2) — площадь третьего яруса (под агератум)
5) 25 000 : 10 000 ∙ 80 = (25 000 ∙ 80) : 10 000 = 2 000 000 : 10 000 = 200 (куст.) — агератума
6) 90 000 — 40 000 — 25 000 = 50 000 — 25 000 = 25 000 (см2) — площадь второго яруса (под виолу)
7) 25 000 : 10 000 ∙ 70 = (25 000 ∙ 70) : 10 000 = 1 750 000 : 10 000 = 175 (куст.) — виолы
Ответ: 9 м2; 240 кустиков тагетесов, 175 кустиков виолы и 200 кустиков агератума.