5 класс. Математика. Виленкин. Учебник. Часть 1. Проверьте себя (страница 129)
Ответы к заданию Проверьте себя на странице 129
Проверочная работа №1
Номер 1.
Выберите из чисел 2, 5, 6, 10, 18, 180, 291, 2323, 3450, 15 555, 20 605, 33 333, 333 333 числа, которые:
а) делятся на 2;
2, 6, 10, 18, 180, 3450.
б) делятся на 10;
10, 180, 3450.
в) не делятся на 2;
5, 291, 2323, 15 555, 20 605, 33 333, 333 333.
г) делятся на 5, но не делятся на 10;
5, 15 555, 20 605.
д) кратны 9;
18, 180, 333 333.
е) делятся на 3, но не делятся на 9;
6, 291, 3450, 15 555, 33 333.
ж) делятся на 2 и на 3.
6, 18, 180, 3450.
Номер 2.
Можно ли найти число, которое делится на 10, но не делится на 2?
Такого числа не существует, так как любое число, которое делится на 10, делится и на 2 тоже.
Номер 3.
На столе лежат рисунки, которых больше 60, но меньше 80. Эти рисунки можно сложить в папки по 6 либо по 8 рисунков. Сколько рисунков на столе?
72 рисунка, так как число 72 больше 60, но меньше 80 и делится и на 6 и на 8.
Номер 4.
Вычислите:
(26 ∙ 652 — 16 ∙ 652) : 5 + 504 ∙ 4 : 9 = 652 ∙ (26 — 16) : 5 + 2016 : 9 = 652 ∙ 10 : 5 + 2016 : 9 = 6520 : 5 + 2016 : 9 = 1304 + 224 = 1528
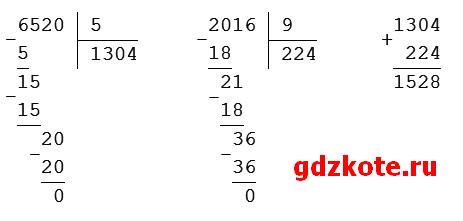
Проверочная работа №2
Номер 1.
Можно ли 234 человека рассадить в 5 автобусов поровну?
Нельзя, так как 234 не делится на 5 нацело.
Номер 2.
Запишите все делители числа 60.
1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
Номер 3.
Известно, что двузначное число делится на 9 и состоит из одинаковых цифр. Выпишите все такие числа.
99
Номер 4.
Известно, что нечетное трехзначное число делится на 5 и состоит из цифр 0, 5 и 7. Что это за число?
705
Номер 5.
Катя купила 9 тетрадей и потратила на покупку 357 р. Могло ли такое быть, если цена тетради выражается натуральным числом рублей?
Такого быть не могло, так как 357 не делится на 9 нацело.
Пояснение:
Число делится на 9, если сумма цифр этого числа делится на 9.
3 + 5 + 7 = 19 — не делится на 9, значит, и 357 не делится на 9.
Номер 6.
Не вычисляя суммы, становите, делится ли на 3 каждое из слагаемых и будет ли делиться нацело на 3 их сумма:
Число делится на 3, если сумма цифр этого числа делится на 3.
а) 321 + 459;
321 — 3 + 2 + 1 = 6 — делится на 3
459 — 4 + 5 + 9 = 18 — делится на 3
Значит, сумма чисел 321 и 459 делится на 3.
б) 323 + 4571.
323 — 3 + 2 + 3 = 8 — не делится на 3
4571 — 4 + 5 + 7 + 1 = 17 — не делится на 3
Значит, сумма 323 и 4571 не делится на 3.
Номер 7.
В числе 345* вместо звёздочки поставьте цифру так, чтобы полученное число:
а) делилось на 5;
3450 или 3455
б) делилось на 3 и на 9;
3456
в) делилось на 2, на 3, на 5 и на 10.
3450